生存模型
课程名称:INS212 生存模型 Survival models
课程性质:本学院精算专业学生必修,其他学院选修或根据专业培养方案确定。
学分课时:3学分,48课时
主讲教师:李晋清讲师
所属院系:保险学院 精算与统计系
电话:18610455378, E-mail:02456@uibe.edu.cn
教学对象:全校二年级上学期
考核方式:平时测试内容包括模型建立和R软件编程,共有3次,每次占比10%
期末考试,闭卷考试,笔试。
其中平时3次测试占30%,作业占10%,期末考试占60%
学术诚信:本课程对于学生的学术诚信的要求遵从《对外经济贸易大学学生违纪处分条例》、《对外经济贸易大学学生学习违纪处分实施细则》、《对外经济贸易大学考场纪律》的规定。
教学方式:理论篇占比50%,软件操作编程占比50%。教学中理论与实际案例相结合,应用理论知识建立模型解决实际问题,同时学生要求通过R编程进行模型检验和实际数据分析。
出勤要求:遵从《对外经济贸易大学本科生课堂学习规范》,要求学生关闭一切电子设备;不能无故缺席上课;上课专心听讲,积极参与课堂讨论;课后认真复习课堂上讲授内容,独立完成教师布置的任务;并预习新课。学生缺勤不得多于总课时的四分之一。教师可以根据考勤情况决定学生是否可以参加考试、是否扣分。
一、 课程简介
生存模型是精算专业的必修课。这门课程有四大部分,分别是
(1)应用概率论和统计方法来分析事件发生时间和研究影响事件发生时间的因素,
(2)生命表的制作原理,
(3)风险之间相关性分析,
(3)马尔柯夫模型理论以及马尔柯夫模型在寿险,长期健康险和医疗险定价中的应用。
其中第一部分我们学习三类模型:无参数模型,参数模型和半参数回归模型。第二部分生命表的制作涉及到了死亡率的估计,平滑调整,Lee-Carter以及相关预测模型。第三部分学习多状态模型, 多衰量模型,马尔柯夫链,马尔柯夫跳跃过程和泊松过程。生存模型这门课一半是理论学习,一半是R语言编程进行计算和模型检验,以及实际案例数据分析。
二、教学目标
本课程的定位是:培养学生精算和统计分析思维、激发学生精算和统计兴趣,掌握观察和分析精算问题的正确方法和熟练应用精算模型解决实际问题的能力,为进一步学习精算其他专业课程打下坚实的基础。
本课程的教学目标:通过教学使学生对生存模型的基本概念和基本理论有正确的理解和较深刻的认识,对回归分析、概率分布、统计检验、优化求解、生命表制作和R语言编程有较系统的掌握,掌握观察和分析精算问题的正确方法,初步培养辨析精算理论和应用精算理论解决实际问题的能力。
三、课程学习资料
1.教材
(1).讲师编写的讲义
(2).英国精算师协会CT4讲义
2.参考资料
(1) S.Nadarajah .S.A.A. Bakar (2013). A new package for actuarial survival models. Journal of computational statistics 28 pp. 2139-2160
(2)Chapter 1 and 3 from Kalbfleish, J. D. and Prentice, R. L. (2002), The statistical analysis of failure time data, John Wiley &Sons
(3)Cox, D. R. (1975), ‘Partial likelihood’, Biometrika 62(2), 269-276
(4) Lee , R. D. & Carte, L. R. (1992), Modeling and forecasting U.S. mortality, Journal of the American Statistical Association 87(419), 659-671
(5) Camarda, C. G.(2012), MortalitySmooth: An R package for smoothing Poisson counts with P-splines, Journal of Statistical Software, 50(1), 1-24.
(6) Hyndman, R. J. & Ullah, S.(2007), Robust forecasting of mortality and fertility rates: A functional data approach, Computational Statistics and Data Analysis, 51(10),4942-4956
(7)David C.M.Dickson, Mary R. Hardy & Howard R.Waters (2009) Actuarial mathematics for life contingent risks, Cambridge University Press, pp 242-292
(8)Frees & Wang (2006), Copula credibility for aggregate loss models, Insurance: Mathematics and Economics 38, 360-373
(9)R package ‘ActuDistns’
(10)R package ‘survival’
(11)R package ‘fitdistrplus’
(12)R package ‘demography’
(13)R package ‘MortalitySmooth’
(14) R package ‘lifecontingencies’
(15)R package‘markovchain’
(16)R package‘fCopulae’
四、学习效果
通过本课程的学习,希望达成的学习效果如下:
(1)掌握精算分析中常用的事件发生时间随机变量的概率分布表达式,并应用分布进行相关计算。给定概率分布,应用R 语言编程计算相关概率以及生成随机变量。
(2)掌握生存数据类型,区分完全观测到的数据,删失数据和截断数据(通过案例数据进行区分),应用R语言编程生成删失数据和截断数据。
(3)掌握参数模型的建立,建立基于完全观测到的数据,删失数据和截断数据。通过最大似然估计法进行模型参数估计。理解并推导最大似然估计的渐近统计性质。应用R语言编写估计方程并进行检验。
(4)基于完全观测到的数据,删失数据和截断数据,进行无参数建模,应用模型进行相关的概率估计。理解概率估计的渐近统计性质。应用R语言编写无参数概率估计方程,通过生成真实值进行模型检验。
(5)理解半参数回归模型,掌握如何把实际问题转化为半参数回归模型来分析。应用最大偏似然估计法估计回归模型中的参数,理解最大偏似然方程建立的理论依据,和最大偏似然估计的渐近统计性质。应用R程序包对实际案例数据进行半参数回归分析,通过R语言编程来进行参数估计的检验。
(6)掌握计算估计的方差和置信空间。编写R程序进行计算,并通过分析R生成的数据进行模型检验。
(7)掌握生命制作原理和死亡率估计方法,应用统计方法进行死亡率估计平滑。估计基于历史数据,理解生命表的预测模型。分析时实际数据时,应用R程序包进行统计平滑,参数估计和模型预测。
(8)理解多状态模型。学会如何应用多状态模型进行案例分析,掌握多状态模型的应用。应用Kolmogrov’s方程和Thiele’s微分方程计算状态转移概率和产品定价,掌握解微分方程的数值方法。编写R程序进行计算。
(9)理解随机过程基本概念,熟悉马尔柯夫链,并掌握其性质和应用。推导马尔柯夫链Chapman-Kolmogorov 方程,分析马尔柯夫链时间齐次性。掌握多减量模型,应用模型建立多减量表。编写R程序进行实证分析,编写R方程建立多减量表。
(10)了解掌握时间齐次马尔柯夫跳跃过程和时间非齐次马尔柯夫跳跃过程,理解状态转移率及强度矩阵,掌握Kolmogorov 前向微分方程和后向微分方程,应用线性微分方程和矩阵特征值和特征向量计算转移概率。应用跳跃过程解决实际问题。编写马尔柯夫跳跃过程R程序进行实证分析,编写R方程进行模型参数估计。
五、 教学进度以及内容
第一周
事件发生时间的概率分布模型
【教学目的与要求】
第一周是基础篇,介绍生存模型中的基本符号和函数,以及事件发生时间的概率分布。要求学生掌握概率分布R 程序包,编写R程序生成随机变量。
【主要内容】
1.1 精算符号以及函数
1.1.1 事件发生时间的生存函数
1.1.2 事件发生时间的死亡函数
1.1.3 死亡率精算定义
1.2 Complete生命期望
1.3 Curtate 生命期望
1.4 事件发生时间的概率分布
1.4.1 生存函数
1.4.2 危险函数
1.5 死亡率法则
1.5.1 Gompertz’Law
1.5.2 Makehame’s Law
1.5 概率分布的R程序包应用
1.6 编写R程序生成随机变量
【教学总时数】 3
【阅读】
(1)讲义第一章
(2) S.Nadarajah .S.A.A. Bakar (2013). A new package for actuarial survival models. Journal of computational statistics 28 pp. 2139-2160
(3)R package ‘ActuDistns’
【作业与思考题】
1.识记:
Pareto distribution, Beta distribution, Lognormal distribution, Weibull distribution, Gamma distribution, Exponential distribution, Log-logistic distribution. Gompertz’s law, Makehame’s law
2.领会:
(1) 理解各个概率分布有何区别?
(2)应用每个概率分布的依据是什么?
(3)生命期望推导
(4)生命时间方差
(5)Complete生命期望与Curtate 生命期望之间关系
3.运用:
(1)给定一个随机变量的概率分布,推导生命期望,剩余生命服从分布,Complete生命期望与Curtate 生命期望
(2)给定Gompertz’Law或Makehame’s Law, 计算相关的生存概率
(3)给定危险函数数学表达式,推导积累危险函数,生存函数和密度函数,计算生存概率。
4.例题:
Suppose that the force of mortality for a lifetime ![]() is given by
is given by

第二周
事件发生时间的统计分布估计
【教学目的与要求】
本周内容向学生展示了如何用无参数和全参数的统计模型对事件发生时间的分布进行估计。要
学生掌握生存数据类型,区分完全观测到的数据,删失数据和截断数据分布。理解最大似然估
法,KME估计和ANE估计。掌握估计的统计渐进性质,做数学推导。
【主要内容】
2.1 生存数据的特点
2.1.1 左删失数据
2.1.2 右删失数据
2.1.3 区间删失数据
2.1.4 截断数据分析
2.2 删失和截断数据分析模型
2.3 无参数统计模型
2.3.1 KM估计
2.3.2 NA估计
2.4 经验估计
2.5 离散危险率估计
2.6 全参数统计模型
2.7 最大似然估计法
【教学总时数】 3
【阅读】
(1)讲义第二章
(2)Chapter 1 and 3 from Kalbfleish, J. D. and Prentice, R. L. (2002), The statistical analysis of failure time data, John Wiley &Sons
【作业与思考题】
1.识记:
删失数据,截断数据,删失指示函数,全参数模型,最大似然估计,KME估计,NAE估计
2.领会:
(1)基于删失数据和截断数据的模型构造
(2)估计的统计渐近性质。
(3)KME估计与NAE估计之间的关系。
(4)当生存时间为离散情况下危险函数的推导。
3.运用:
(1)已经全参数模型的最大似然估计,计算删失和截断时间。
(2)给定一个随机变量概率分布,进行R编程计算其死亡率,生存概率并画图。编出的程序与R程序包进行数值比较。
(3)给定一个离散随机变量的概率分布,计算其死亡率,根据样本数据计算死亡率的最大似然估计,计算生命期望值的最大似然估计。
4. 例题:
An insurance broker observed the lifetimes of 48 clients holding a 10-year term assurance policy.
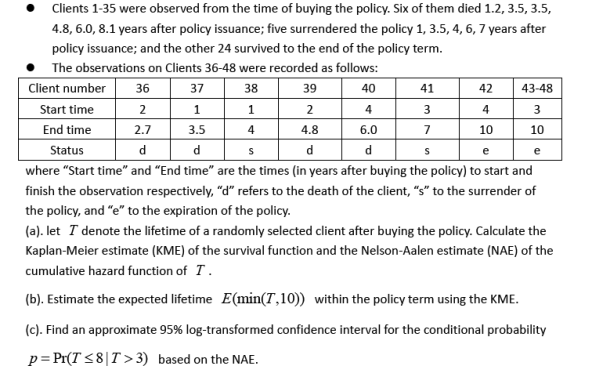
第三周
估计的方差和置信区间
【教学目的与要求】
本周是对第二周推导出来的估计进行方差和置信区间计算,要求学生掌握方差公式数学推导并且
编写R程序计算进行方差计算和置信区间建立。
【主要内容】
3.1 经验估计方差和置信区间
3.2 KME方差和置信区间
3.3 NAE 方差和置信区间
3.4 参数最大似然估计方差矩阵和置信区间
3.4.1 Fisher信息矩阵
3.4.2 Delta方法
3.4.3 Log-transformed置信区间
3.5 编写R程序计算进行方差计算和置信区间建立
【教学总时数】 3
【阅读】
讲义第三章
【作业与思考题】
1.识记:
经验估计方差,KME方差,NAE 方差,Fisher信息矩阵,Delta方法和Log-transformed置信区间
2.领会:
(1)经验估计方差推导
(2)KME和NAE 方差公式理解
(3)Fisher信息矩阵理解
(4)Delta公式推导
(5)Log-transformed置信区间公式推导
3.运用:
(1)给定一组删失截断数据,计算KME和NAE 方差和生存概率方差
(2)计算参数模型中参数最大似然估计方差,应用delta方法计算最大似然估计函数方差并建立置信区间
(3)给定一组删失截断数据,计算生存概率和积累危险函数log-transformed 置信区间
4. 例题:
In a survival data analysis, the life time ![]() of a certain species is modeled by an inverse Weibull distribution with cdf
of a certain species is modeled by an inverse Weibull distribution with cdf


第四周
编写R程序估计生存分布
【教学目的与要求】
本周要求学生使用反函数法编写R程序生成删失截断数据,使用递推法编写R程序计算KME和NAE估计和方差,建立log-transformed置信区间。通过计算生成随机变量生存概率真实值,对比真实值和估计值,进行方法检验。
【主要内容】
4.1编写R程序生成生存时间,和删失截断数据,
4.2 编写R程序计算KME估计和log-transformed置信区间并画图
4.3 编写R程序计算NAE估计和log-transformed置信区间并画图
4.4编写R程序计算生成随机变量生存概率真实值,对比真实值和估计值,进行方法检验。
【教学总时数】 3
【阅读】
讲义第四章
【作业与思考题】
1.识记:
R方程编写,loop应用,逻辑方程,随机变量生成器
2.领会:
(1)R方程编写步骤
(2)R程序逻辑应用
(3)R程序LOOP应用
(4)R作图
3.例题:参看生存模型上机指导实验三-无参数估计。
第五周-第六周
半参数回归模型
【教学目的与要求】
应用PH模型来分析影响事件发生时间的因素,要求学生掌握回归模型理论,最大偏似然估计
法,理解最大偏似然估计的统计渐近性。应用R程序包分析实际数据进行影响因子估计,编写R
程序进行参数估计模拟,通过比较模拟参数期望和和方差来检验模型。
【主要内容】
5.1 PH模型
5.2 PH模型下全参数危险函数回归分析
5.3 PH模型下无参数危险函数回归分析
5.3.1 最大偏似然估计
5.3.2 估计方差计算
5.3.3 基础分布估计
5.4 统计检验
5.4.1 LR统计检测
5.4.2 Wald’s统计检测
5.5应用R程序包分析实际数据进行影响因子估计和统计检测
5.6编写R程序进行参数估计模拟
【教学总时数】 6
【阅读】
(1)讲义第五章
(2)Cox, D. R. (1975), ‘Partial likelihood’, Biometrika 62(2), 269-276
(3)R package ‘survival’
(4)R package ‘fitdistrplus’
【作业与思考题】
1.识记:
PH模型,基础分布,回归分析,LR统计检测,Wald’s统计检测
2.领会:
(1)PH回归模型在实务中的应用
(2)全参数危险函数回归分析与无参数危险函数回归分析的区别
(3)LR统计量渐近分布
(4)Wald’s统计量渐近分布
(5)基础分布的Brewlow估计
3.运用:
(1)给定一组实际数据,分析影响事件发生时间的影响因子,推导最大偏似然方程,计算最大偏似然估计,计算置信区间,计算相关的生存概率,统计检测。
(2)PH模型在寿险定价中的应用
(3)PH模型在信用风险分析中的应用
4. 例题:
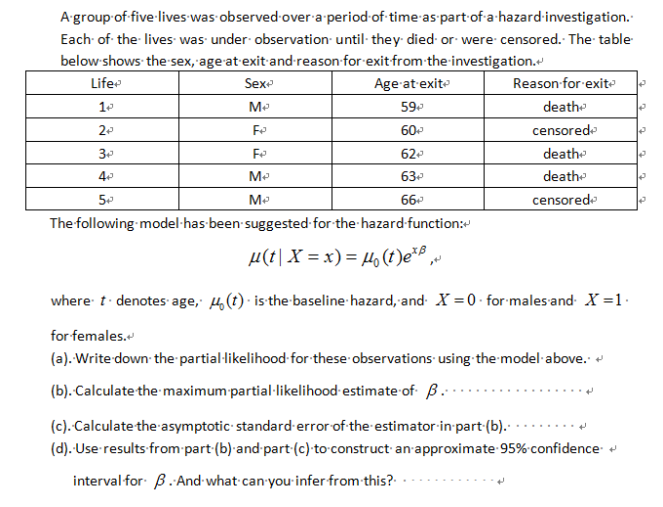
第七周-第九周
生命表制作
【教学目的与要求】
生命表应用在寿险产品的定价和准备金的计算上。通过学习,学生明白生命表的制作原理,并进
行生命表预测此外,学生也要求通过编写R程序进行生命表的制作。
【主要内容】
6.1 风险暴露
6.1.1 Weighted constrained penalized regression splines
6.1.2 Two-dimensional P-splines
6.2 死亡率模型
6.2.1 二项式模型
6.2.2 泊松模型
6.3 一般情形下的死亡率估计
6.4 统计平滑调整
6.4.1 公式法
6.4.2 标准表格法
6.4.3 平滑检验
6.5统计检测
6.5.1 Chi-square 检测
6.5.2 Standard deviation检测
6.5.3 Signs检测
6.5.4 Cumulative deviations检测
6.5.5 Runs检测
6.5.6 Serial correlations检测
6.7 Lee-Carter模型和相关的预测模型
6.7.1 Lee-Carter 模型
6.7.2 Lee-Mille模型
6.7.3 Booth-Maindonald –Smith模型
6.7.4 Hyndman-Ullah模型
6.7.5 Robust Hyndman-Ullah模型
6.7.6 Weighted Hyndman-Ullah模型
6.8 生命表制作
6.9 应用软件R程序包,自编程序进行生命表制作。
【教学总时数】 9
【阅读】
(1) 讲义第六章
(2) Lee , R. D. & Carte, L. R. (1992), Modeling and forecasting U.S. mortality, Journal of the American Statistical Association 87(419), 659-671
(3) Camarda, C. G.(2012), MortalitySmooth: An R package for smoothing Poisson counts with P-splines, Journal of Statistical Software, 50(1), 1-24.
(4) Hyndman, R. J. & Ullah, S.(2007), Robust forecasting of mortality and fertility rates: A functional data approach, Computational Statistics and Data Analysis, 51(10),4942-4956
(5)R package ‘demography’
(6)R package ‘MortalitySmooth’
(7) R package ‘lifecontingencies’
【作业与思考题】
1.识记:
统计平滑原理,Lee-Carter预测模型,泊松模型,二项式模型,Chi-square 检测,Serial correlations检测
2.领会:
(1)生命表制作步骤
(2)生命表的不同预测模型比较
(3)各种统计检测的比较
3.运用:
(1)应用统计平滑法对实际数据进行统计平滑分析
(2)应用预测模型进行生命表预测
(3)应用统计检测对平滑进行拟合检验
4.例题:

第十周
马尔柯夫链
【教学目的与要求】
本周属于基础篇,学习为计算状态之间转移概率做基础。要求学生掌握随机过程的基本概念,随
机过程类别,马尔柯夫链性质和应用, 和马尔柯夫链中的参数估计。要求学生应用R程序 ’markovchain’ 包进行计算和分析。
【主要内容】
7.1 随机过程概要
7.1.1 随机过程类别
7.1.2 平稳性
7.1.3 增量
7.1.4 可测集合
7.2马尔柯夫链性质
7.3 Chapman-Kolmogorov 方程
7.4 时间齐次马尔柯夫链
7.5 平稳分布
7.5.1 存在性
7.5.2 唯一性
7.5.3 周期性
7.6 马尔柯夫链应用
7.7 应用R进行马尔柯夫链分析
【教学总时数】 3
【阅读】
(1)讲义第七章
(2)R package‘markovchain’
【作业与思考题】
1.识记:
随机过程平稳性和增量,马尔柯夫链性质,马尔柯夫链长期行为
2.领会:
(1)马尔柯夫链状态转移概率计算
(2)马尔柯夫链长期状态转移概率极值计算
(3)时间齐次马尔柯夫链特征
(4)Chapman-Kolmogorov 方程
3.运用:
(1)医疗险中医疗费用估计
(2)平稳分布的唯一性和周期性
(3)白色噪音
(4)随机游走
(5)泊松过程和复合泊松过程
4.例题:

第十一周-十二周
马尔柯夫跳跃过程
【教学目的与要求】
让学生学习推导和计算时间齐次马尔柯夫跳跃过程下状态转移的概率,推导和计算时间非齐次马尔柯夫跳跃过程下状态转移的概率。通过学习泊松过程理解马尔柯夫跳跃过程的应用。要求学生编写R程序建立泊松过程,复合编写R程序建立泊松过程和Levy 过程
【主要内容】
8.1 时间齐次马尔柯夫跳跃过程
8.1.1 Chapman-Kolmogorov状态转移概率
8.1.2状态转移率及强度矩阵
8.1.3 Kolmogorov 前向微分方程
8.1.4 Kolmogorov 后向微分方程
8.1.5 应用线性微分方程计算转移概率
8.1.6 应用矩阵特征值和特征向量计算转移概率
8.2 时间非齐次马尔柯夫跳跃过程
8.2.1 Chapman-Kolmogorov状态转移概率
8.2.2状态转移率
8.2.3 Kolmogorov 前向微分方程
8.2.4 Kolmogorov 后向微分方程
8.2.5 状态占有概率
8.2.6 在离开时间的状态转移分析
8.2.7 跳跃链
8.2.8 状态到达时间的期望值
8.2.9 Kolmogorov 方程的积分形式
8.3 泊松过程
8.3.1 时间齐次泊松过程
8.3.2 到达间隔
8.3.3时间齐次泊松过程的一些性质
8.3.4 时间非齐次泊松过程
8.3.5 编写R程序建立泊松过程
8.3.6 编写R程序建立复合泊松过程
8.3.7 编写R程序建立Levy过程
【教学总时数】 6
【阅读】
讲义第八章
讲义第九章
【作业与思考题】
1.识记:
马尔柯夫跳跃的时间齐次性,马尔柯夫跳跃的时间非齐次性,Kolmogorov 前向微分方程
,Kolmogorov 后向微分方程,线性微分方程,矩阵特征值和特征向量,时间齐次泊松过程
时间非齐次泊松过程
2.领会:
(1)强度矩阵推导
(2)Kolmogorov 前向微分方程推导
(3)Kolmogorov 后向微分方程推导
(4)Kolmogorov 前向微分方程和Kolmogorov 后向微分方程区别
3.运用:
(1)状态占有概率推导
(2)跳跃链分析
(3)状态到达时间的期望值计算
(4)Kolmogorov 方程的积分推导
4. 例题:
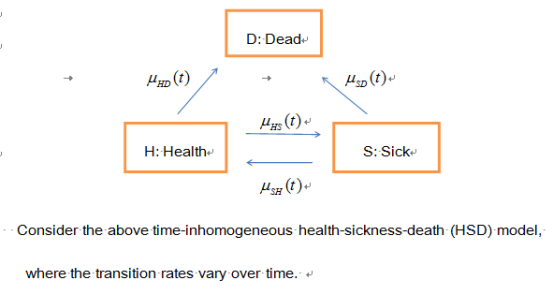

第十三周
马尔柯夫跳跃过程应用
【教学目的与要求】
本周内容是在第十周到第十二周的理论基础上,应用到解决实际问题中去。要求学生掌握马尔柯夫跳跃模型,根据实际问题建立多状态模型,编写R程序进行数据分析和产品定价。
【主要内容】
9.1 两状态的马尔柯夫跳跃过程
9.2模型估计
9.3 混合模型
9.4 联合分布
9.4.1 最大似然估计
9.4.2 最大似然估计的统计渐近性
9.5 多状态模型
9.5.1健康-生病-死亡 三状态模型
9.5.2 伤残险
9.5.3 长期健康护理险
9.6 转移概率的数值解法
9.7 Thiele’s 微分方程
9.8 多衰量模型
9.8.1 建立多衰量表
9.8.2 从相关率推导相互独立率
9.8.3从互相独立率推导相关率
9.9 编写R程序进行多衰量模型和多状态模型分析
【教学总时数】 3
【阅读】
(1)讲义第十章
(2)David C.M.Dickson, Mary R. Hardy & Howard R.Waters (2009) Actuarial mathematics for life contingent risks, Cambridge University Press, pp 242-292
【作业与思考题】
1.识记:
健康-生病-死亡 三状态模型,混合模型,联合分布,伤残险模型,多衰量模型基本构造
2.领会:
(1)转移概率数值算法
(2)人寿保单价值计算
(3)Thiele’s 微分方程数值计算
(4)Thiele’s 微分方程一般形式
(5)状态持续时间非整数分析
3.运用:
(1)多衰量模型下状态转移概率计算和产品定价
(2)多衰量表建立
4.例题:


第十四周-第十五周
Copulas模型
【教学目的与要求】
在实务中,风险之间都是有相关性,过多的相互独立假设会使得计算结果不准确。本周讲解Copula模型来分析风险之间的相关性。要求学生理解Copula模型建立的理论基础,编写R程序对实际数据中可能蕴含的风险相关性进行分析。
【主要内容】
10.1 Copulas定义及基本概念
10.2 Sklar’s Representation理论
10.3 Copulas性质
10.3.1 Survival copulas
10.3.2 Dual and co-copulas
10.3.3 Functional invariance
10.3.4 Tail dependence
10.4 Archimedean Copulas家族
10.4.1 定义
10.4.2 Frailty模型
10.4.3 Gumbel Copulas, Frank Copulas, Clayton Copulas
10.4.4 包含 Archimedean Copulas的密度函数
10.5 Elliptical Copulas家族
10.5.1 Gaussian Copulas
10.5.2 Student Coupulas
10.6 编写R程序进行分析
10.6.1 Copulas 拟合
10.6.2 基于实际数据,Copulas选择
【教学总时数】 6
【阅读】
(1)讲义第十一章
(2)R package‘fCopulae’
(3)Frees & Wang (2006), Copula credibility for aggregate loss models, Insurance: Mathematics and Economics 38, 360-373
【作业与思考题】
1.识记:
联合分布,Sklar’s theorem, 边际分布,多维随机变量分布,Copulas概念
2.领会:
(1)考虑风险相关性,考虑两维变量分布建立,比如 Bivariate Pareto distribution
(2)Copulas上限分析
(3)实际数据观测,考虑Copulas选择
(4)考虑Copulas,多维随机变量联合函数建立
(5)不同Copulas函数区别
3.运用:
(1)已知Copulas, 推导条件概率分布
(2)已知Copulas给出的边际分布,推导联合分布
4.例题:
Joe’s copula is given by

第十六周
总复习
撰写人:李晋清
2016年3月